SpinDrops

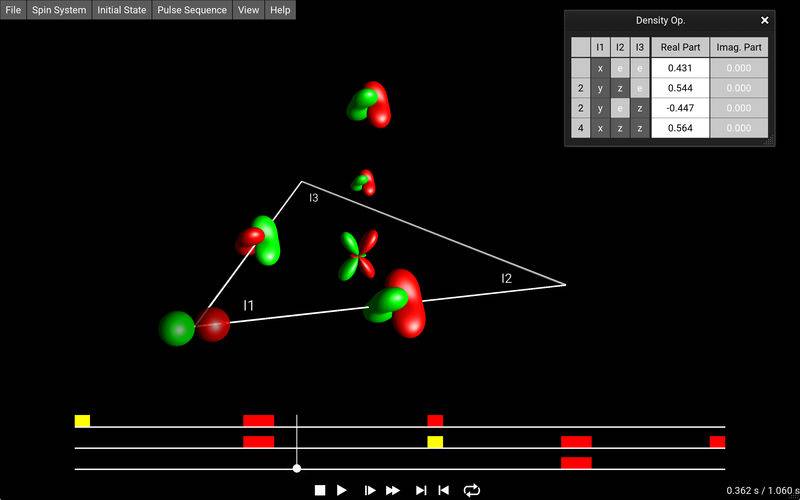
SpinDrops provides a novel approach to understanding magnetic resonance experiments and the underlying spin dynamics. The app teaches fundamental concepts of modern NMR spectroscopy through numerous examples and an online tutorial. The simple graphical interaction helps develop intuition of the mode of action and the design of pulse sequences. Rich dynamics of spin systems (up to three coupled spins) can be explored interactively. The app uses the DROPS representation to depict arbitrary spin states intuitively, yet also with theoretic rigor. This representation is a generalization of the Bloch vector picture and provides a natural, one-to-one mapping between arbitrary spin states and so-called „droplets“. Features of SpinDrops include: - Customizable systems consisting of one, two or three spins 1/2. - Arbitrary Initial states can be defined or chosen from predefined lists. - Pulse sequences can be defined or selected from a list of pre-installed typical homonuclear and heteronuclear experiments, including individual 90° and 180° pulses, Hahn echoes, INEPT, DEPT, isotropic mixing, excitation of three-spin order and of multiple quantum coherence. - Real-time simulations of spin dynamics can be interactively visualized using the graphical DROPS representation, which maps quantum mechanical operators to three-dimensional shapes based on spherical harmonics. This makes it possible to visualize abstract concepts such as anti-phase coherence, multiple-quantum order and coherence transfer. Additional information can be found at www.spindrops.org: - Extensive help is provided, including detailed tutorials, examples, challenges and information on the mathematical background of the DROPS visualization. - Tutorials show how to define a desired initial state, how to create a new pulse sequence, and how to control the simulation and the graphical DROPS display. Furthermore, the properties of the DROPS visualization are explained and the interpretation of characteristic droplets is discussed. The shapes representing Cartesian product operators are discussed and it is shown how the coherence order of an operator is reflected in the shape and color of the corresponding droplet. - Examples and challenges illustrate the interpretation of droplets, their symmetry properties, the evolution of single and coupled spins, the refocussing of offsets and couplings, spectral editing, and coherence transfer.